The joy of joymetry-2

Previous

We can prove the theorem very simply, as follows.

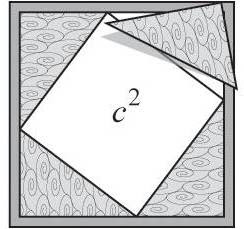
Let’s go back to the tilted square sitting on the hypotenuse.

At an instinctive level, this image should make you feel a bit uncomfortable. The square looks potentially unstable, like it might topple or slide down the ramp. And there’s also an unpleasant arbitrariness about which of the four sides of the square gets to touch the triangle.

Guided by these intuitive feelings, let’s add three more copies of the triangle around the square to make a more solid and symmetrical picture:

Let’s recall what we’re trying to prove: that the tilted white square in the picture above (which is just our earlier “large square”— it’s still sitting right there on the hypotenuse of the four triangles along the corners of the bigger square) has the same area as the small and medium squares put together. But where are those other squares? Well, we have to shift some triangles around to find them.

Think of the picture above as literally depicting a puzzle, with four triangular pieces wedged into the corners of a rigid puzzle frame.

In this interpretation, the tilted square is the empty space in the middle of the puzzle. The rest of the area inside the frame is occupied by the puzzle pieces.

Now let’s try moving the pieces around in various ways. Of course, nothing we do can ever change the total amount of empty space inside the frame — it’s always whatever area lies outside the pieces.

The brainstorm, then, is to rearrange the pieces like this:

All of a sudden the empty space has changed into the two shapes we’re looking for — the small square and the medium square. And since the total area of empty space always stays the same, we’ve just proved the Pythagorean theorem!

This proof does far more than convincing; it illuminates. That’s what makes it “elegant.”

Next